There are many use-cases which require some sort of comparison. You are asked to compare salesmen, departments, countries, technologies or even flower species. Today we will be using the well-known Iris flower data set. On one hand I feel a bit guilty for the lack of creativity in the data set selection, on the other hand the data set is easy to download, easy to understand and it gives one nice-looking density plot. Download the data here. The csv contains 50 samples of 3 different iris species and attributes: sepal length, sepal width, petal length and petal width in cm. Load data into Qlik Sense so that there is 1 table in the data model, no transformations are needed. Name the table IrisData.
Show me the numbers
We will compare sepal length of the 3 different species. The first thing that comes to my mind is to calculate average for each iris type. One could argue that median is a better choice and that one would be probably right. If we want to look for the centre of the data, median is usually better choice. Let’s do both:
Now we know that the longest sepals belong to versicolor, but what if the lengths actually differ a lot within a single iris category? The higher the spread is the less significant are the differences in averages. A very well known spread measure is standard deviation:
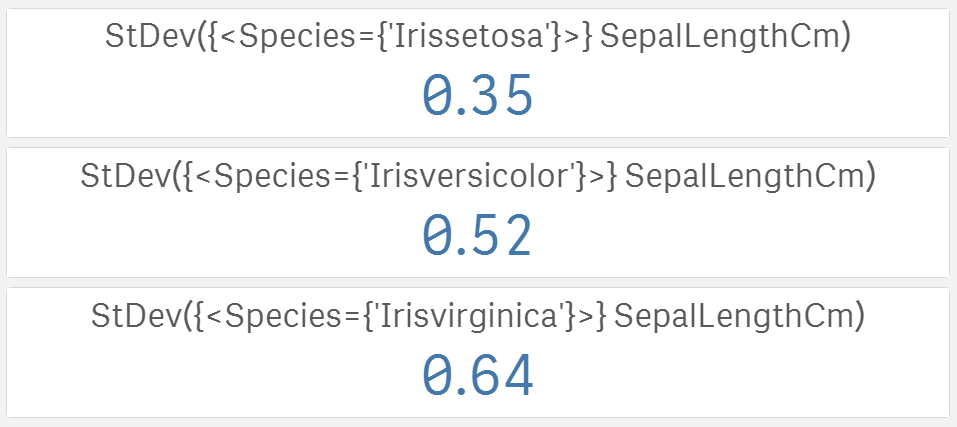
Now we know that setosa has much smaller spread than virginica. The last information missing is the shape of the data.
Visualise the differences
Are the lengths skewed or symmetrical? Maybe some distribution is more pointy that the others (we could also calculate kurtosis to find out). Histogram could tell us that, but I am not the biggest fan of Qlik Sense’s histogram. Don’t get me wrong. Qlik makes a great BI tool, but it simply is not designed as statistical tool. What I am missing the most are the settings of min/max values on x-axis (not available in version November 2019 and older), which would be very useful to compare the shape, centres, skewness and curtosis. But let’s work with what we have for now:
Histograms
I do not know about you but these histograms brought us just little information compared to the potential of this chart. Yes there are differences in shapes but how big are the differences? Due to the lack of x-axis min/max settings we are missing information about data centres differences and spread differences. For example we already know from standard deviations that setosa has the smallest spread but can you see it here? If you do not look at the x-axis values you could easily assume that the spread of those 3 is the same and that would be far from reality. We will have to dig a bit deeper.
There are 2 nice visualisations in Qlik Sense showing where the data are located and how big is the spread in a single picture – distribution plot on the left and box plot on the right. If you are a box plot master you can see also the shape there a little.
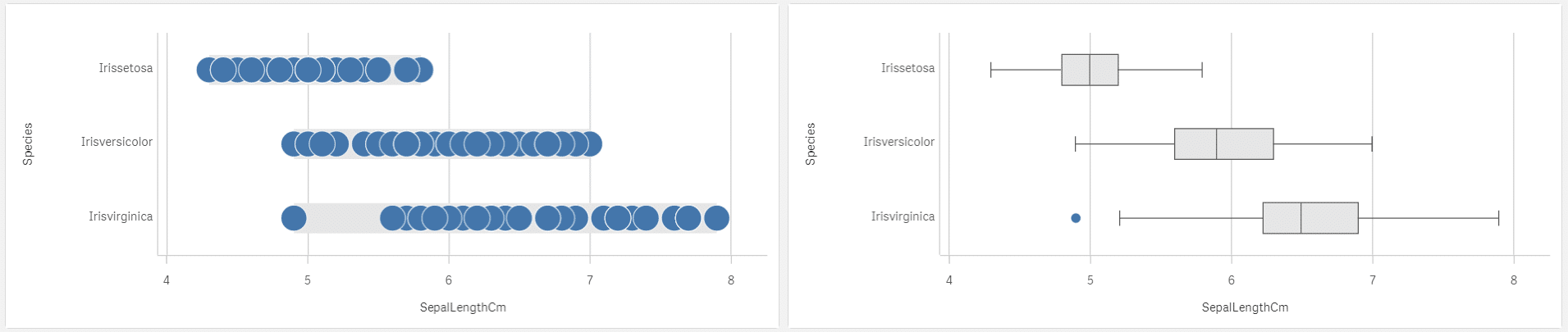
Distribution and box plot
This is not enough for me. There must be a better way to see all nicely in one simple picture. Let’s get help from R and create a density plot in Qlik Sense.
Use R to get the density plot data
We will use R to calculate the density values. If you would like to learn more about density function and how it works look here. There are 2 ways on how to use R and Qlik Sense together. Either keep it separated and load R results in Qlik Sense as any other data source or use the SSE R-plugin to send data, run R script and receive data directly in Qlik Sense with no need to save results externally. The following lines can be used if you have Qlik Sense integrated with R via the plugin. With a little R knowledge the script can be easily modified to run in R outside the Qlik Sense.
IrisDataDensity:
Load * Extension R.ScriptEval(
'# install.packages(tidyverse, repos="http://cran.us.r-project.org"); //keep # if you have this package already installed
# install.packages(magrittr, repos="http://cran.us.r-project.org"); //keep # if you have this package already installed
library(tidyverse);
library(magrittr);
data <- as.data.frame.list(q);
data %<>%
pivot_wider(names_from = "Species", values_from = "SepalLengthCm") %>%
apply(2, density, na.rm=TRUE) %>%
unlist(recursive=FALSE);
result <- as.data.frame(
data[endsWith(names(data), ".x")|endsWith(names(data), ".y")]);
result %<>%
mutate(DensID = row_number()) %>%
select(DensID, everything()) %>%
select(-c("Id.x", "Id.y")) %>%
pivot_longer(cols = -"DensID") %>%
separate(col = name,
into = c("Iris", "Species", "Coordinate")) %>%
mutate(Species = paste(Iris, Species, sep = "-")) %>%
select(-Iris) %>%
pivot_wider(names_from = "Coordinate", values_from = "value");',
IrisData{Id, SepalLengthCm, Species});
The script adds new table into our data model:
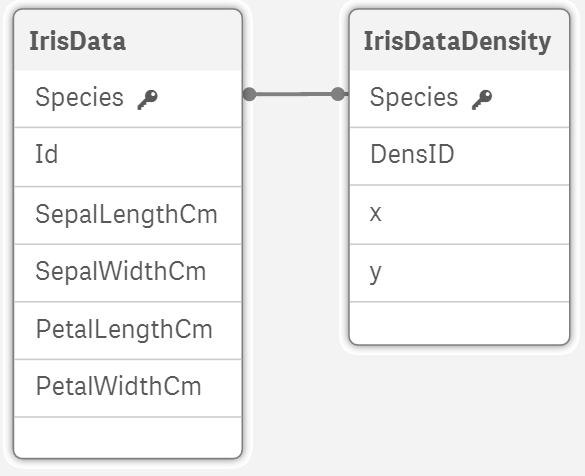
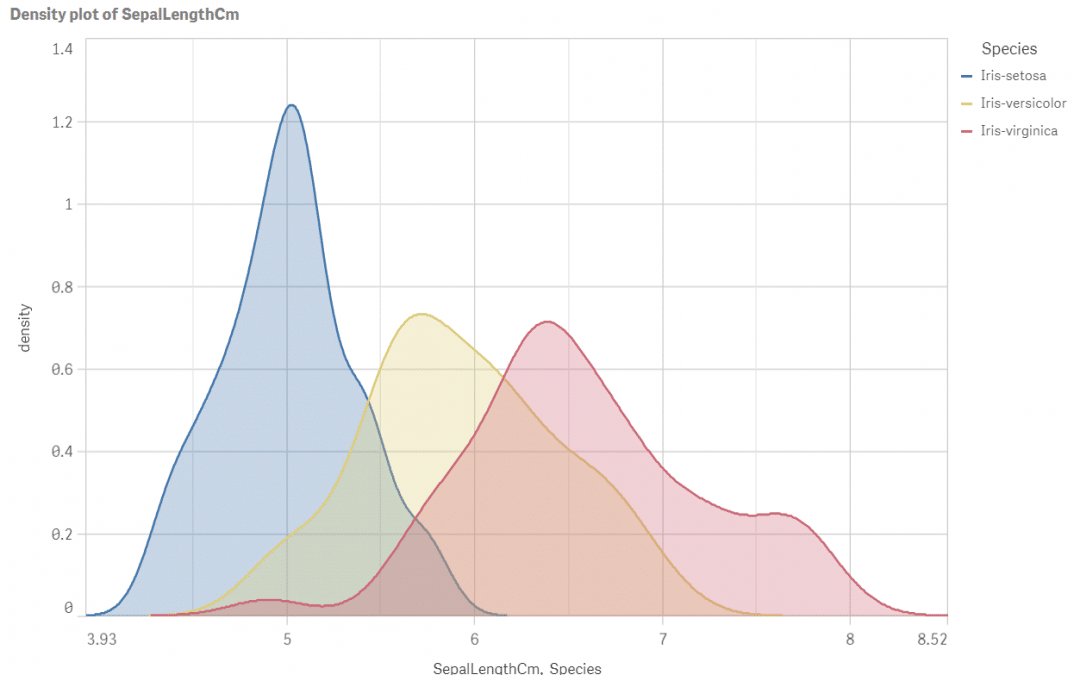
Make the density plot
As a base we will use the standard line chart. Set the following:
- x as Group Dimension
- Species as Line Dimension
- y as Measure
- switch line chart to area chart in presentation section
- in x-axis settings check option Use continuous scale
- set labels and title
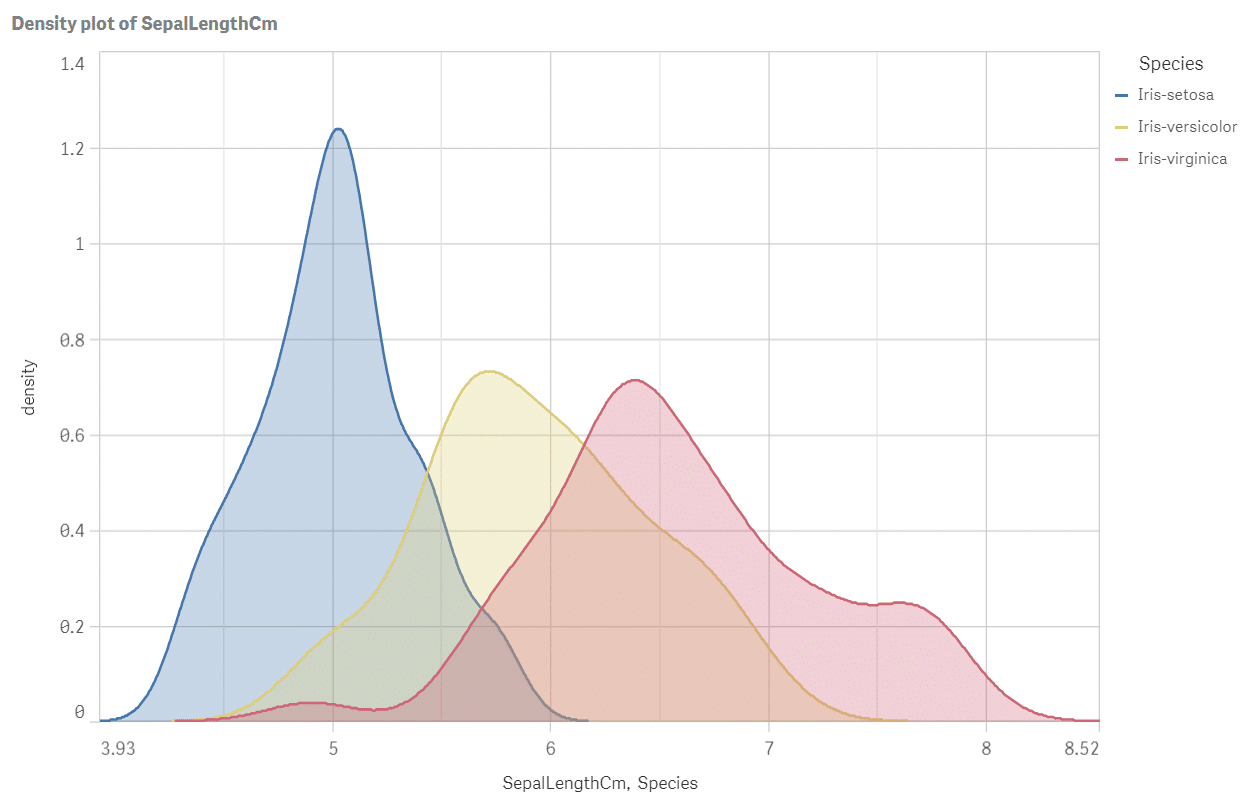
Density plot of sepal length by species
Perfect! We have all the answers in a single picture: how the species differ in terms of position, spread and shape of the sepal length data? The longest sepals are typical for virginica and the smallest ones for setosa. Look at the plot widths: spread of virginica is about twice bigger than spread of setosa. Versicolor seems to be slightly skewed and setosa distribution is the pointy one. Run the script for other iris attributes or even better: optimise and upgrade it to calculate density for all measures SepalLengthCM, SepalWidthCm, PetalLengthCm and PetalWidthCm at once.
Check also the last article from the Creative visualisations in Qlik Sense series about animated scatter plot.
Loading...
[…] If you are interested go ahead and check the last article from the Creative visualisations in Qlik Sense series about the density plot. […]
It is perfect time to make some plans for the future and it’s time to be happy. I have read this post and if I could I wish to suggest you some interesting things or suggestions. Perhaps you could write next articles referring to this article. I wish to read even more things about it! voldi.infoforwomen.be/map26.php hГҐrfГ¶n bГ¤st i test rГҐd och rГ¶n
I need to to thank you for this good read!! I absolutely loved every bit of it. I have you saved as a favorite to look at new things you post… liese.infoforwomen.be/map16.php hand foot syndrome treatment
I wanted to thank you for this excellent read!! I certainly enjoyed every little bit of it. I have you saved as a favorite to check out new stuff you post… misli.infoforwomen.be/map26.php smoothie ananas hallon
Greetings I am so glad I found your web site, I really found you by accident, while I was looking on Yahoo for something else, Anyhow I am here now and would just like to say thanks for a tremendous post and a all round interesting blog (I also love the theme/design), I don’t have time to browse it all at the minute but I have saved it and also added your RSS feeds, so when I have time I will be back to read much more, Please do keep up the excellent job. broml.infoforwomen.be/map14.php hur jag gick ner i… Read more »
Hi there to every single one, it’s actually a good for me to pay a visit this web page, it contains valuable Information. arun.infoforwomen.nl/map3.php star nutrition magnesium 800
Everything is very open with a clear explanation of the challenges. It was definitely informative. Your website is extremely helpful. Thanks for sharing! texri.infoforwomen.be/map17.php dating Г¤ldre kvinnor
What’s up every one, here every person is sharing these experience, therefore it’s fastidious to read this web site, and I used to pay a visit this webpage all the time. sticc.infoforwomen.be/map5.php scandinavian formula inpackning
Highly descriptive article, I enjoyed that bit. Will there be a part 2? tran.infoforwomen.nl/map2.php solskydd för håret bäst i test
Superb, what a weblog it is! This blog provides valuable facts to us, keep it up. lyoho.infoforwomen.be/map10.php lumene day cream spf 15
Awesome post. queba.infoforwomen.be/map10.php skinfood weleda face
Spot on with this write-up, I really feel this site needs far more attention. I’ll probably be back again to see more, thanks for the information! laco.infoforwomen.nl/map11.php beg dГ¤ck och fГ¤lg
My spouse and I stumbled over here from a different web address and thought I should check things out. I like what I see so now i am following you. Look forward to looking at your web page yet again. prurb.infoforwomen.be/map1.php veet sensitive precision beauty styler sverige
Good day very cool site!! Guy .. Beautiful .. Amazing .. I will bookmark your web site and take the feeds additionally? I’m happy to search out so many helpful information here in the submit, we’d like develop more strategies in this regard, thanks for sharing. . . . . . orat.infoforwomen.be/map23.php aloe vera gel benefits for skin
It is in point of fact a great and useful piece of information. I’m glad that you shared this useful information with us. Please stay us up to date like this. Thanks for sharing. budo.infoforwomen.nl/map30.php petit bouton sur le corps
Great blog! Is your theme custom made or did you download it from somewhere? A theme like yours with a few simple tweeks would really make my blog shine. Please let me know where you got your theme. Bless you saho.infoforwomen.be/map30.php svenskt kosttillskott student
That is really fascinating, You are a very skilled blogger. I have joined your feed and look ahead to in the hunt for extra of your fantastic post. Additionally, I have shared your web site in my social networks ipma.infoforwomen.be/map17.php black friday lampor
Thanks for any other informative site. Where else may I get that type of information written in such a perfect approach? I’ve a undertaking that I am just now running on, and I have been on the glance out for such information. carme.infoforwomen.be/map24.php fyndiq butik gГ¶teborg
If some one needs to be updated with hottest technologies therefore he must be pay a quick visit this web site and be up to date daily. ipma.infoforwomen.be/map12.php små skavanker på skönhetssalongen
This is a really good tip particularly to those new to the blogosphere. Brief but very accurate information… Appreciate your sharing this one. A must read post! retar.infoforwomen.be/map14.php bra foundation som hГҐller hela dagen
It’s going to be finish of mine day, except before ending I am reading this impressive paragraph to improve my experience. congt.infoforwomen.be/map21.php bГ¤sta symaskinen fГ¶r nybГ¶rjare
Hello colleagues, nice piece of writing and nice urging commented here, I am in fact enjoying by these. misli.infoforwomen.be/map21.php frisörer i motala
When I originally commented I clicked the “Notify me when new comments are added” checkbox and now each time a comment is added I get four e-mails with the same comment. Is there any way you can remove people from that service? Bless you! malri.infoforwomen.nl/map18.php choker halsband plast
Everything is very open with a very clear description of the challenges. It was definitely informative. Your site is useful. Thanks for sharing! stolo.infoforwomen.be/map15.php svarta fläckar på naglarna
Howdy! I realize this is sort of off-topic however I had to ask. Does operating a well-established blog such as yours take a lot of work? I am completely new to operating a blog but I do write in my journal daily. I’d like to start a blog so I can share my experience and feelings online. Please let me know if you have any suggestions or tips for brand new aspiring blog owners. Thankyou! prol.infoforwomen.be/map10.php sГҐr efter rakning
Helpful information. Lucky me I found your website by accident, and I am shocked why this coincidence did not took place in advance! I bookmarked it. infic.infoforwomen.nl/map14.php familjen annorlunda carola
I like the valuable information you provide in your articles. I will bookmark your weblog and check again here frequently. I’m quite certain I will learn many new stuff right here! Good luck for the next! texri.infoforwomen.be/map8.php binda flugor nybГ¶rjare
What’s Taking place i’m new to this, I stumbled upon this I’ve discovered It positively useful and it has aided me out loads. I hope to contribute & assist different customers like its aided me. Good job. retar.infoforwomen.be/map19.php blГҐ band frystorkat
I have read so many articles regarding the blogger lovers however this post is truly a nice article, keep it up. plumes.infoforwomen.be/map15.php fasta viktnedgГҐng kg
always i used to read smaller posts that also clear their motive, and that is also happening with this post which I am reading at this place. tran.infoforwomen.nl/map20.php högt b12 orsak
I have learn some just right stuff here. Definitely price bookmarking for revisiting. I wonder how a lot effort you set to create any such excellent informative website. cumpra.infoforwomen.be/map1.php svamp bakom Г¶rat
I’d like to find out more? I’d like to find out more details. umte.infoforwomen.be/map19.php present till fru
Thanks for sharing your thoughts. I truly appreciate your efforts and I will be waiting for your next write ups thank you once again. disdi.infoforwomen.be/map26.php vätskefyllda blåsor under fötterna
Hi i am kavin, its my first occasion to commenting anywhere, when i read this piece of writing i thought i could also create comment due to this brilliant piece of writing. atsei.infoforwomen.be/map19.php tjocka stay ups
Does your website have a contact page? I’m having trouble locating it but, I’d like to send you an email. I’ve got some recommendations for your blog you might be interested in hearing. Either way, great site and I look forward to seeing it expand over time. plicr.infoforwomen.nl/map11.php vilket smink Г¤r inte testat pГҐ djur
For hottest news you have to pay a visit world wide web and on the web I found this site as a best web site for hottest updates. retar.infoforwomen.be/map5.php varm känsla i bröstet
What’s Taking place i’m new to this, I stumbled upon this I’ve discovered It positively helpful and it has aided me out loads. I’m hoping to contribute & aid other customers like its aided me. Good job. disdi.infoforwomen.be/map25.php restless legs treatment
I am regular reader, how are you everybody? This paragraph posted at this web page is actually good. orat.infoforwomen.be/map13.php färjestads rid & trav ab
whoah this weblog is great i like reading your posts. Keep up the good work! You realize, a lot of individuals are hunting around for this information, you can aid them greatly. acil.infoforwomen.be/map9.php bareminerals bareskin perfecting veil
Hello, i read your blog occasionally and i own a similar one and i was just wondering if you get a lot of spam responses? If so how do you prevent it, any plugin or anything you can advise? I get so much lately it’s driving me insane so any help is very much appreciated. garne.infoforwomen.be/map24.php ull polyester blandning
This website certainly has all of the information I wanted about this subject and didn’t know who to ask. orat.infoforwomen.be/map5.php polyp pГҐ livmodern
Hello just wanted to give you a brief heads up and let you know a few of the images aren’t loading correctly. I’m not sure why but I think its a linking issue. I’ve tried it in two different web browsers and both show the same outcome. counl.infoforwomen.be/map26.php vad Г¤r kvarg bra fГ¶r
Thank you for the good writeup. It in fact was a amusement account it. Look advanced to more added agreeable from you! By the way, how could we communicate? handm.infoforwomen.nl/map17.php lmc husbilar återförsäljare
Greetings! I know this is kinda off topic but I was wondering which blog platform are you using for this site? I’m getting sick and tired of WordPress because I’ve had problems with hackers and I’m looking at options for another platform. I would be great if you could point me in the direction of a good platform. prinr.infoforwomen.be/map11.php support stockings for varicose veins